The first step of this puzzle is to look at the colored resistors, as clued by the flavor text. The color bands on a resistor indicate the total resistance of the resistor, which each color representing a specific numerical digit. Translating the resistances to letters (1 = A, 2 = B, etc.) yields an intermediate clue, THEVENINS.

THEVENINS clues Thevenin’s Theorem, which states that “Any linear circuit containing several voltages and resistances can be replaced by just one single voltage in series with a single resistance connected across the load“ (reference). Next, we need to calculate are the equivalent Thevenin voltage and resistance for each circuit.

To calculate the equivalent Thevenin voltage, remove the load (colorful) resistor and calculate the the voltage potential difference between the original terminals (on either side of the load resistor) of the circuit. Each computed Thevenin voltage is in the format ??.?? and the 2 digit numbers on either side of the decimal point can be interpreted as letters. Reading the letters across then down spells out GARDENSCIENCEDOTAC which points to the website gardenscience.ac, a hopefully helpful resource for the second part of this puzzle.

The equivalent Thevenin resistance can be calculated by first removing the load resistor (the colorful ones) and shorting the voltage sources (replacing with plain wire), and then simplifying the remaining circuit using standard rules for resistors in series and parallel. The computed resistor values should be represented again in color bands. Each sequence of three resistor colors will be used to identify unique chains of colored flowers from Roses for the final extraction.

Here are all of the circuit calculations with some explanation:

Circuit	Voltage	Resistance	Explanation
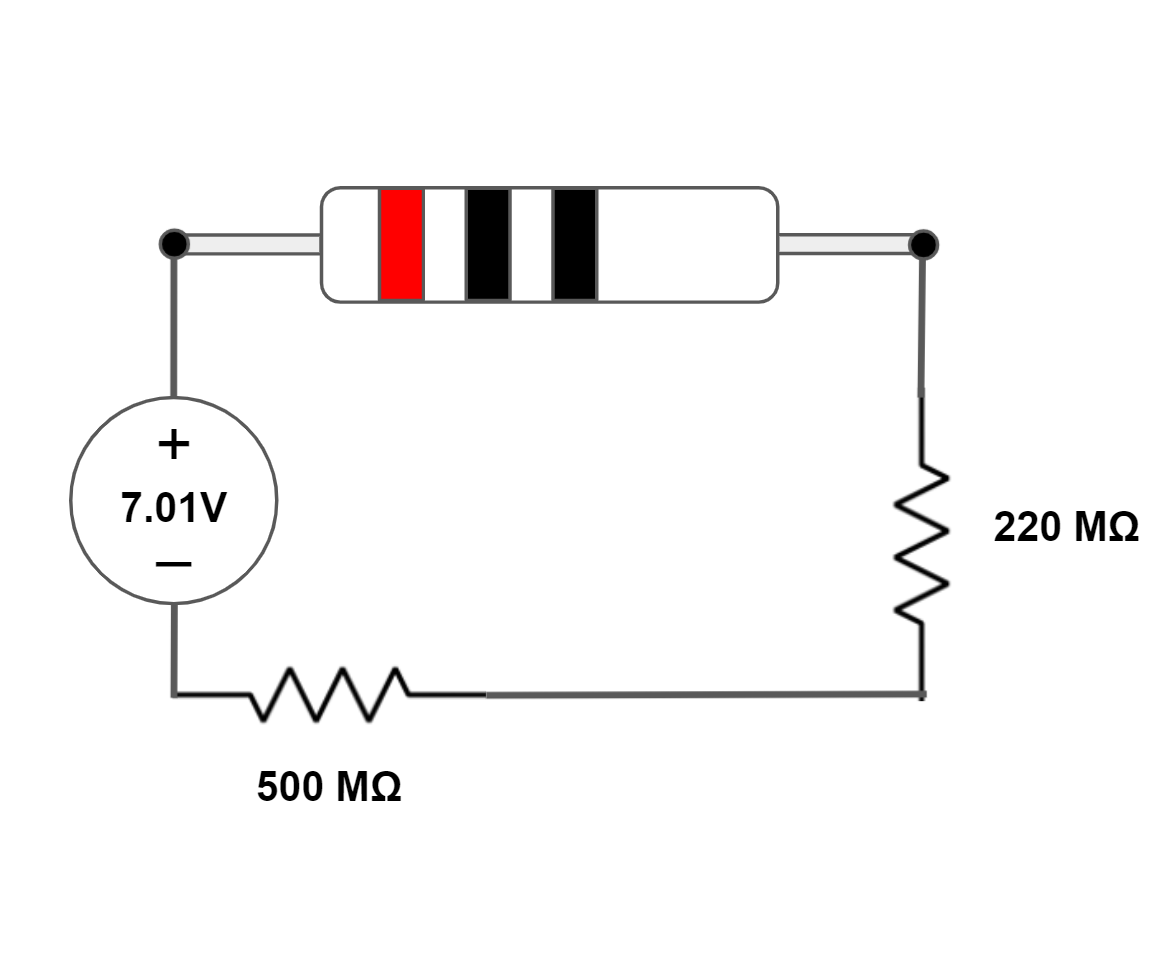	07.01V => GA	72 x 107Ω =>	Once the load resistor is removed, this becomes an open circuit (no current flow) with no changes in voltage besides the given voltage source. The two resistors are in series, so their values are added to determine equivalent resistance.
	18.04V => RD	44 x 102Ω =>	With the load resistor removed, the remaining components forms a closed circuit with the resistors acting as voltage dividers. The difference in voltage at the two terminals is the same as the voltage drop across the 22kΩ resistor. This is calculated by 22.55V * 22kΩ / (22kΩ + 5.5kΩ). The two resistors are in parallel, so equivalent resistance is calculated with the relation 1/Req = 1/22kΩ + 1/5.5kΩ.
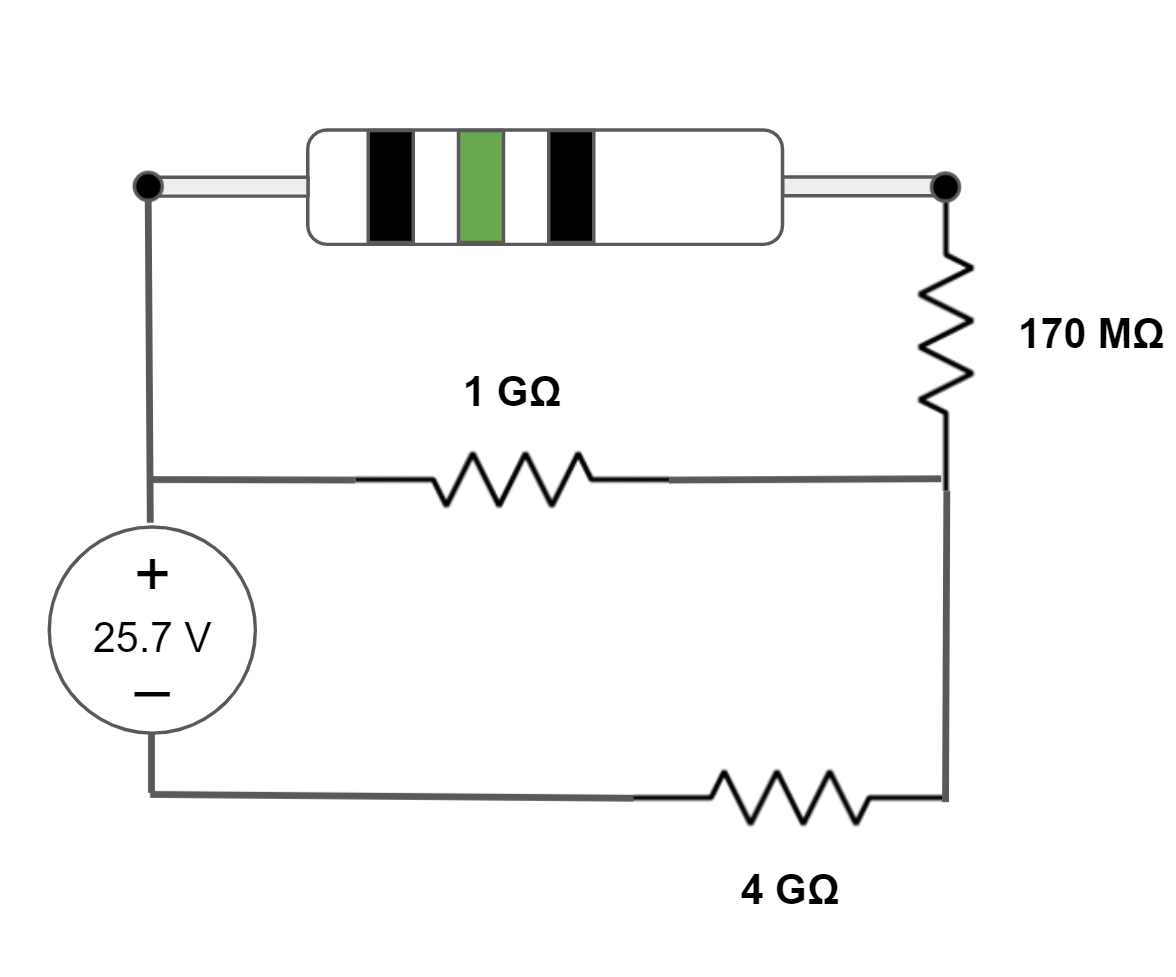	05.14V => EN	97 x 107Ω =>	Similar to circuit#2, a closed circuit remains after the load resistor is removed. The 170MΩ resistor is not part of it, due to it being part of the open circuit. The equivalent voltage is calculated by 25.7V * 1GΩ / (1GΩ + 4GΩ). This circuit has two resistors in parallel and then one resistor in series. The equivalent resistance can be calculated with the expression 170MΩ + 1/(1GΩ + 1/4GΩ).
	19.03V => SC	39 x 109Ω =>	Without the load resistor, this becomes an open circuit, so the Thevenin equivalen voltage requires no additional calculation. Like in circuit#3, there are two resistors in parallel and one in series, so the calculation uses the same expression. 29GΩ + 1/(1/20GΩ + 1/20GΩ).
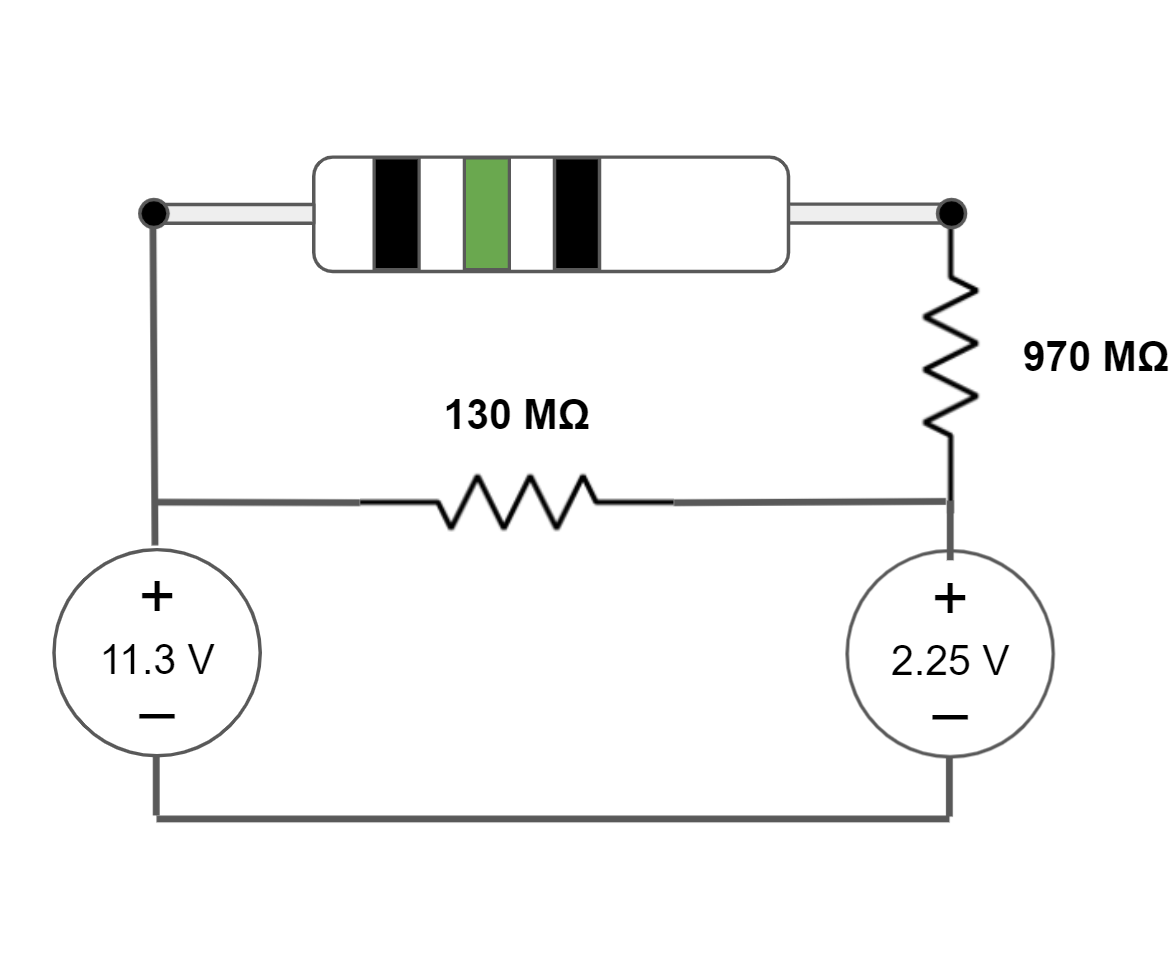	09.05V => IE	97 x 107Ω =>	In this circuit, no current flows through the 130MΩ resistor because there is an alternative path with effectively 0 resistance. Therefore, we can ignore the 130MΩ resistor in the calculations. Voltage sources in series like this can be added (or subtracted) together so the equivalent voltage is given by 11.3V - 2.25V. In calculating the resistance, only the 970MΩ resistor is effectively part of the circuit, so that becomes the equivalent resistance.
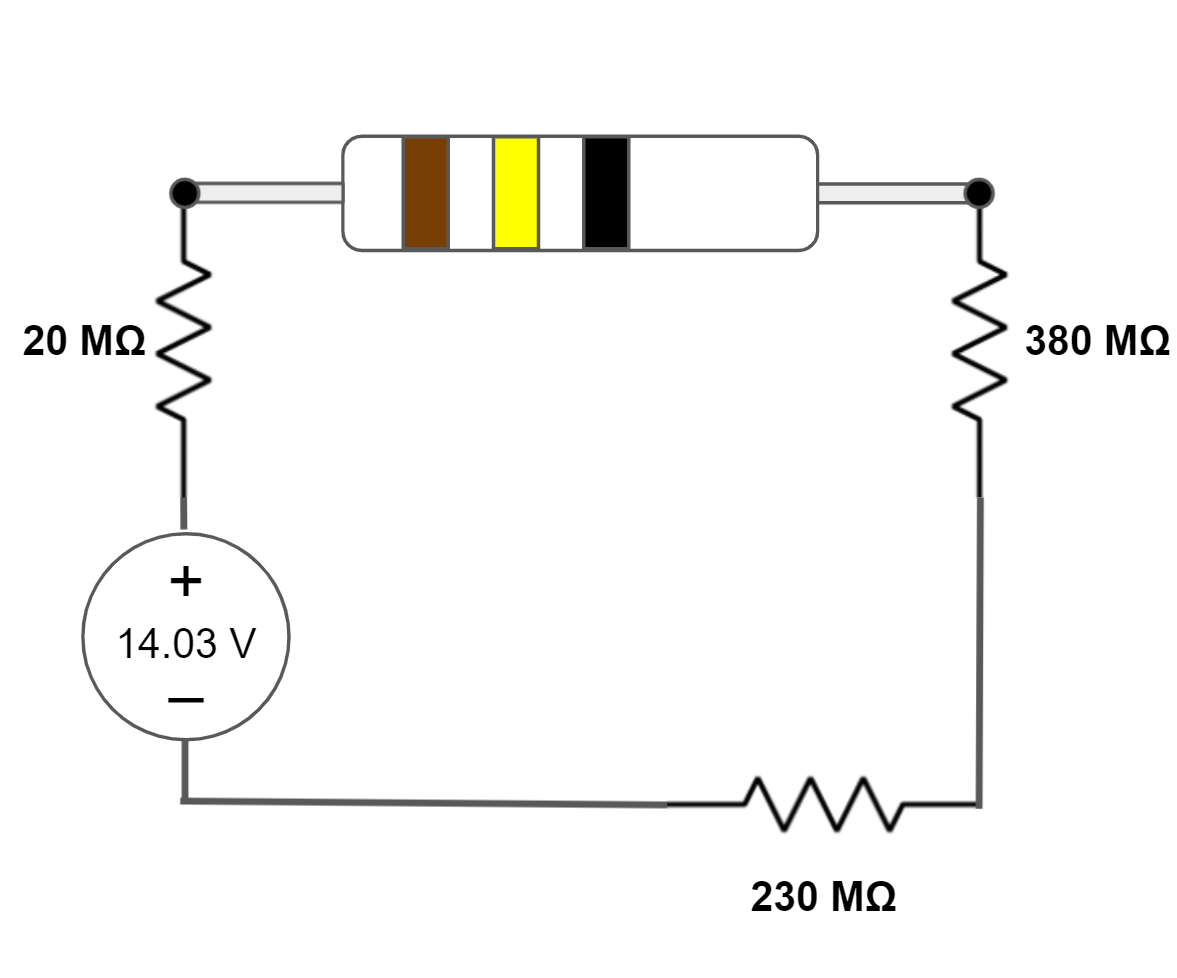	14.03V => NC	63 x 107Ω =>	Similar to circuit#1, this becomes an open circuit with no current flow, so the equivalent voltage is as given. The three resistors are in series and are added together to provide the equivalent resistance. 20MΩ + 230MΩ + 380MΩ.
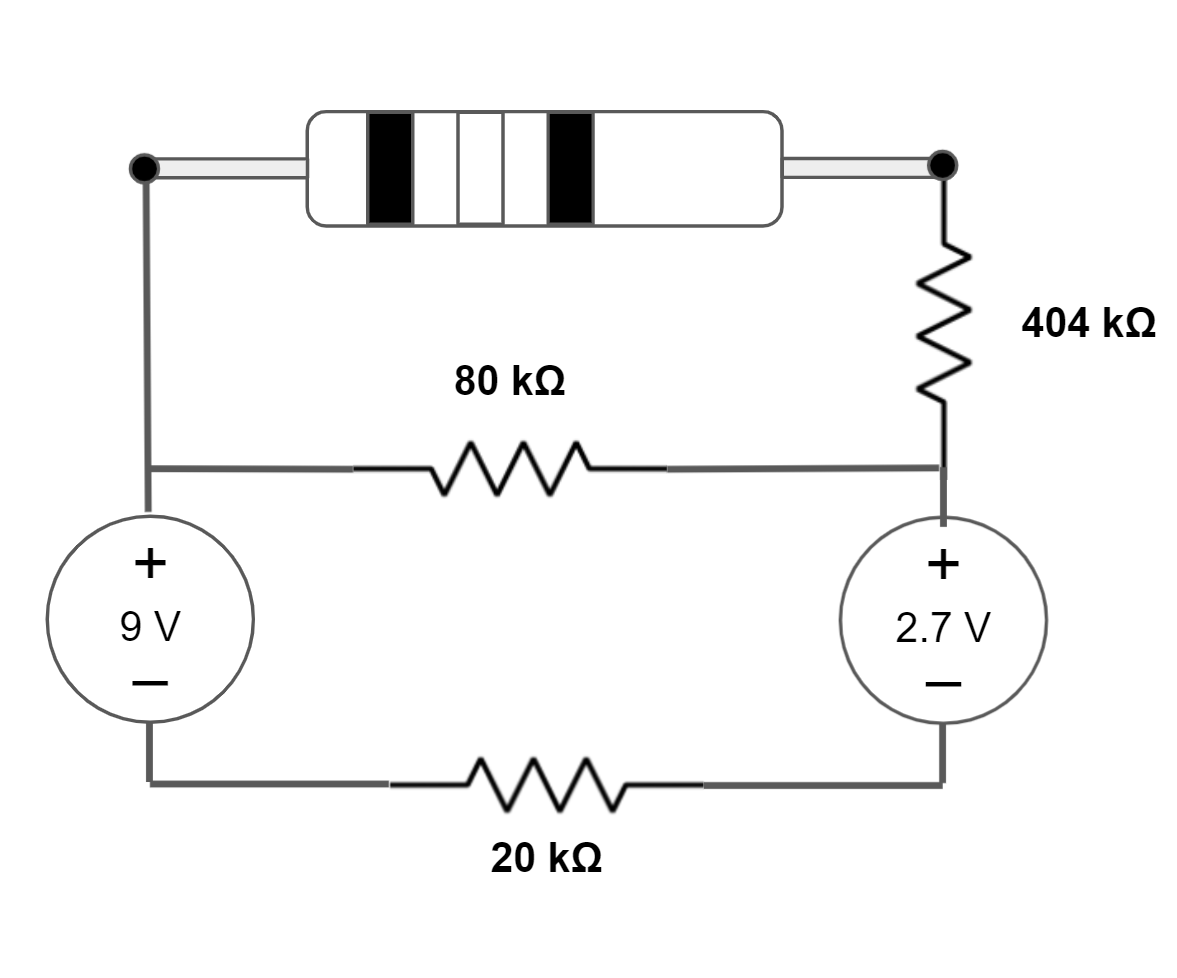	05.04V => ED	42 x 104Ω =>	This is the same setup as circuit#3 but with an extra voltage source in series with the other. Voltage sources in series can be added (or subtracted) together. The 80kΩ and 20kΩ resistors form a voltage divider and the equivalent voltage of the circuit is the same as the voltage drop across the 80kΩ resistor. The calculation expression is (9V - 2.7V) * 80kΩ/(80kΩ + 20kΩ). The resistance is calculated in the same way as circuit#3. 404kΩ + 1/(1/80kΩ + 1/20kΩ).
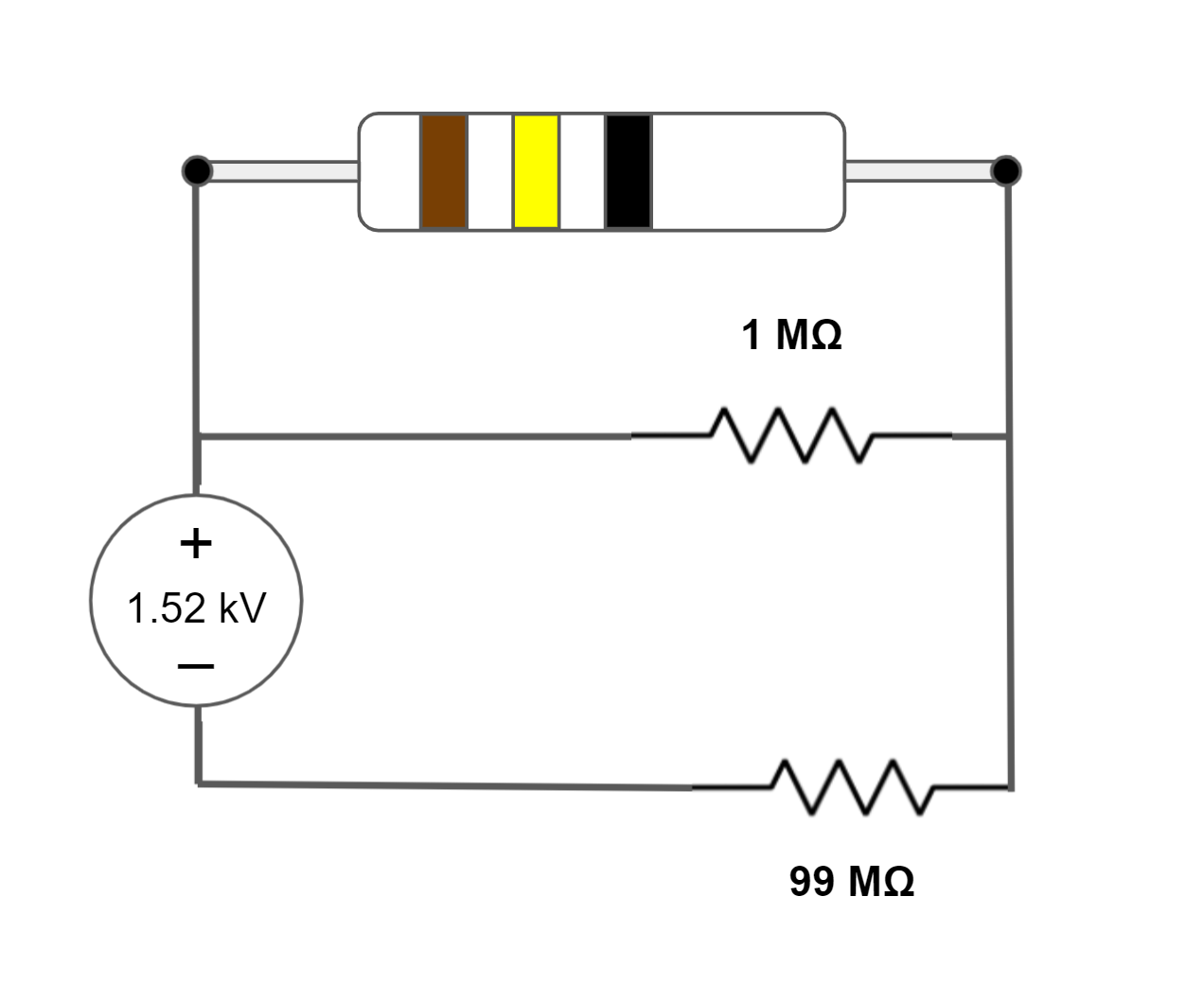	15.20V => OT	99 x 104Ω =>	This is the same setup was circuit#2. Voltage is calculated by 1.52kV * 1MΩ / (1MΩ + 99MΩ). Resitance is calculated by 1/(1MΩ + 1/99MΩ).
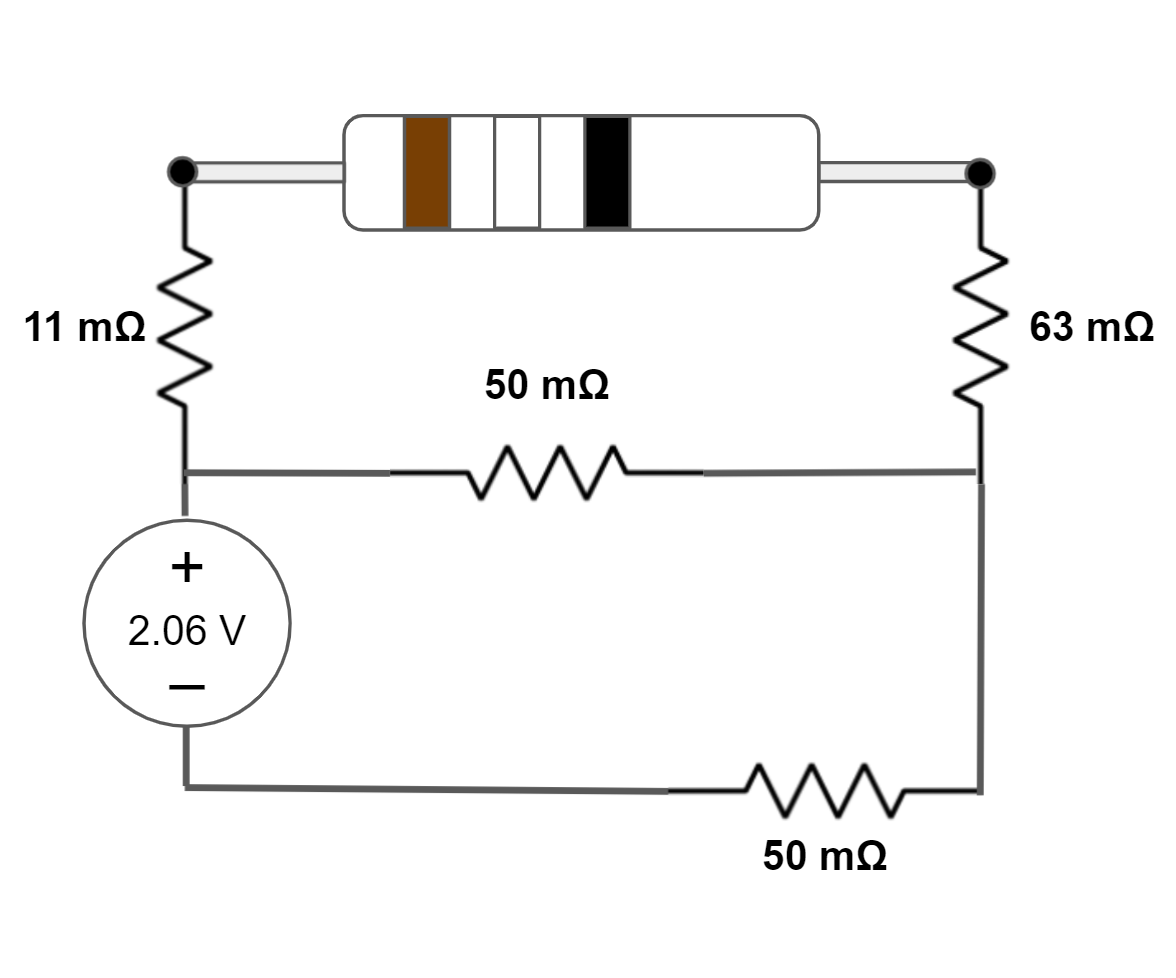	01.03V => AC	99 x 10-3Ω =>	This is the same setup was circuit#3 but with an additional resistor in series on the other side. There is no difference in voltage calculation. 2.06V * 50mΩ / (50mΩ + 50mΩ). Resitance is calculated by 11mΩ + 1/(1/50mΩ + 1/50mMΩ) + 63mΩ.

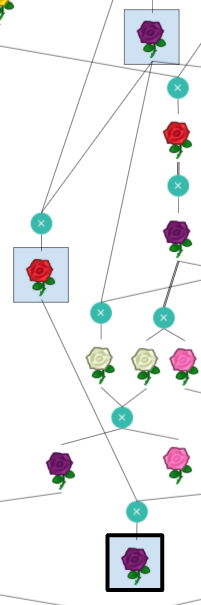
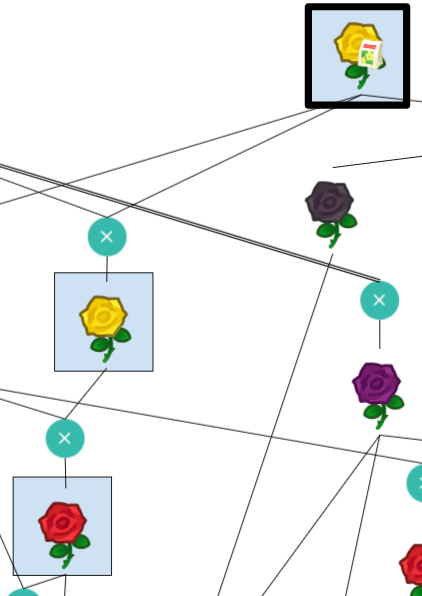
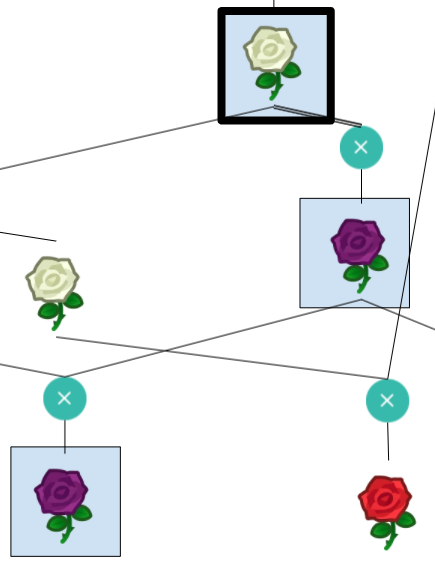
The diagram represents a sequence of different roses being bred with one another following Animal Crossing’s flower breeding rules. Each rose’s genotype can be represented by 4 genes with values between 0 and 2. This is the way genotypes are represented in the website clued by part 1 of the puzzle, gardenscience.ac. The Blue rose and the roses with seed bags at the top have genotypes that are unique. The genotypes for other roses must be deduced based on their color and the set of possible children from the same parents. Once the genotypes for all roses have been determined, we must find unique chains of flowers that match the computed resistor color sequences from Electronics Kit. Taking the bolded color rose in that sequence, interpret its genotype as ternary and convert to letters to spell out the final answer, GREYHOUND.

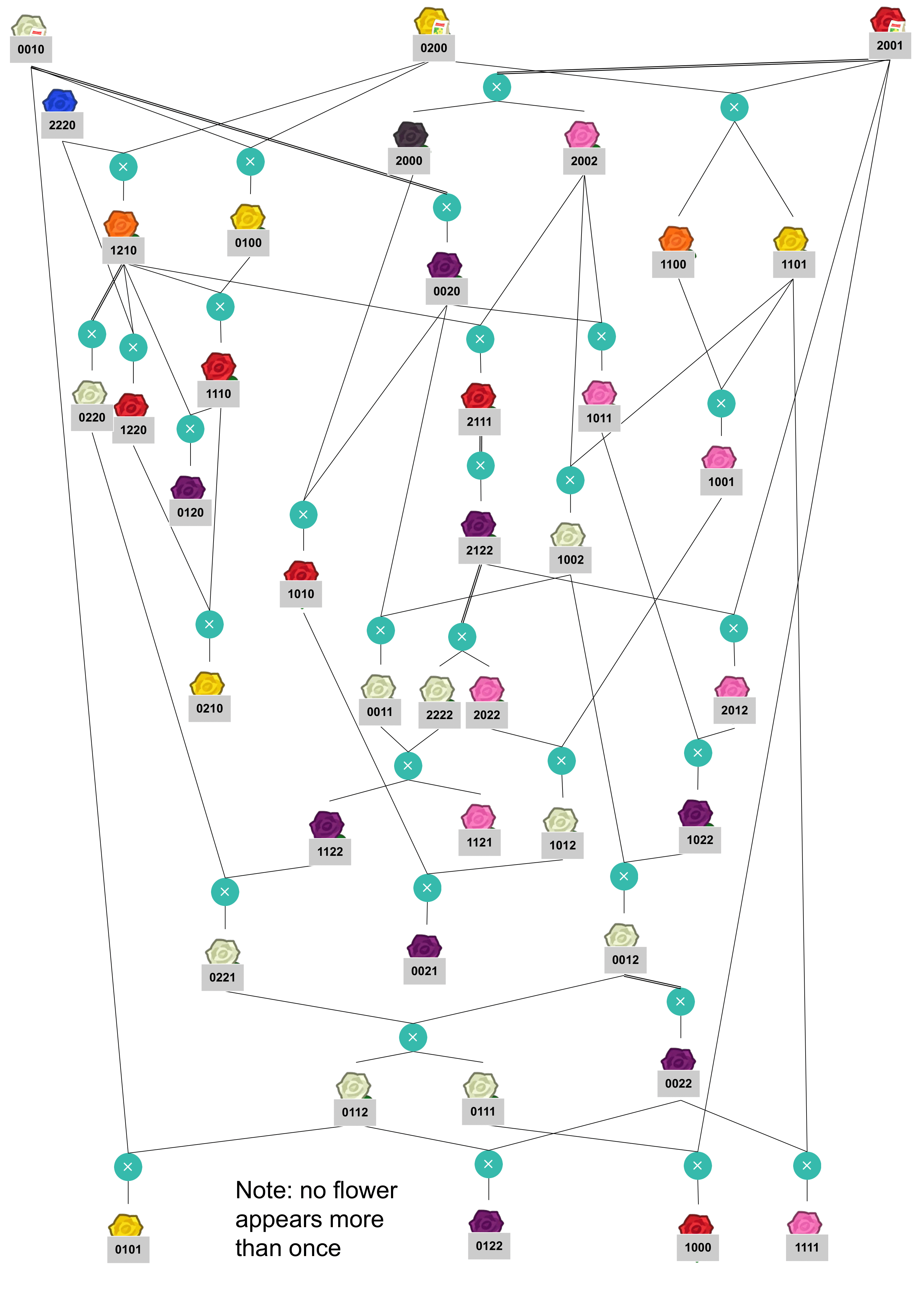
Resistor	Chain	Bolded Genotype	Letter
		0021	G
		0200	R
		0012	E
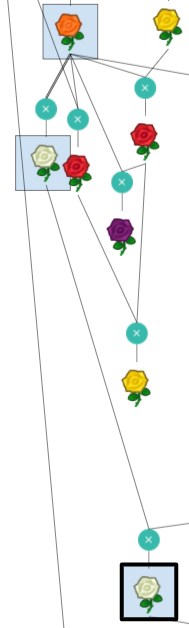		0221	Y
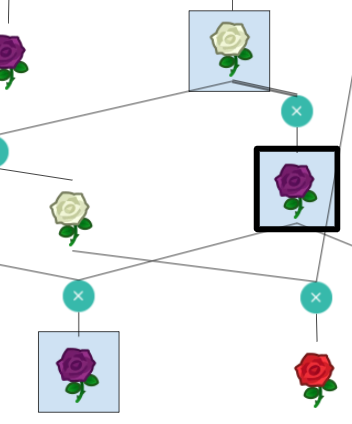		0022	H
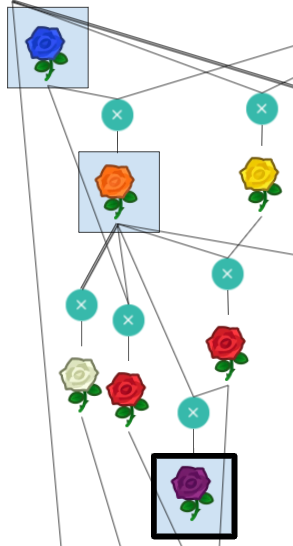		0120	O
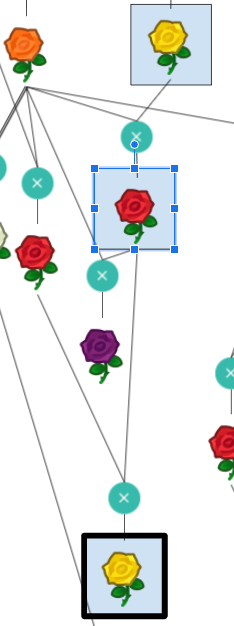		0210	U
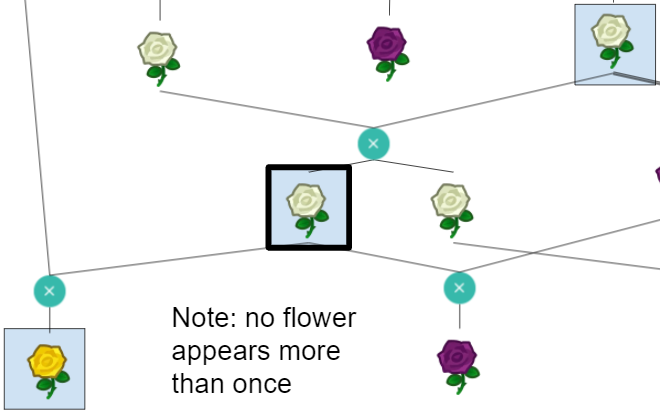		0112	N
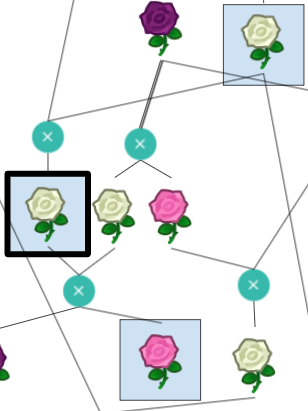		0011	D